Automatic Shape Identification
- June 27th, 2010
- Write comment
As a result of our win at the AUVSI competition, the members of ARC were invited to the John Hopkins APL Small UAV Symposium. During the 5 hour drive back up to Maryland, Alex Ray and I discussed the method that the clever guys over at University of Texas at Austin used for automatic shape identification. Given that we had some time to kill, we decided to try and implement the method ourselves. Detailed here is my attempt.
The method begins with a black and white image showing just the shape in question. For this experiment, black and white images where created as test samples. Additionally some flight imagery was processed to generate the needed black and white images. For this example I will process the image below which has been cropped from an image that ARC captured during the competition run.
% Read in the original image pout = imread(filename); K = rgb2gray(pout); % Create a black and white image of the target K = rgb2gray(pout); bw = im2bw(K, graythresh(getimage)); bw2 = imfill(bw,'holes');
The above code works effectively on this image to create the needed bw image, however this code will not work on all targets. Sharp variations in the background and certain target color combinations can ruin the data. This issue was not further explored because the purpose of this experiment was not finding the targets, but identifying them. It is assumed that the person using this program would provide a good bw target image.
Using this image an outline of the target is created using the code:
% Find the edge of the object K = edge(bw2,'sobel'); [K, map] = gray2ind(K,2);
Then the centroid of the object is found using the code:
% Find the centroid s = regionprops(bw2, 'centroid'); centroids = cat(1, s.Centroid);
With this data collected it is now possible to generate a signature of the target. The signature is simply the distance from the centroid of the target to the outer edge.
% Generate the target's signature dimen = size(K); counter = 1; for i=1:dimen(1) for k=1:dimen(2) if(K(i,k)~=0) % Found an edge point, save the data for this point % Distance from centroid signature(counter,1) = atan2((centroids(1,2)-i),(centroids(1,1)-k)); % Angle signature(counter,2) = (sqrt((centroids(1,2)-i)^2+(centroids(1,1)-k)^2)); % Pixel position signature(counter,3) = i; signature(counter,4) = k; counter = counter +1; end end end % Sort the signature data by angle signature = sortrows(signature);
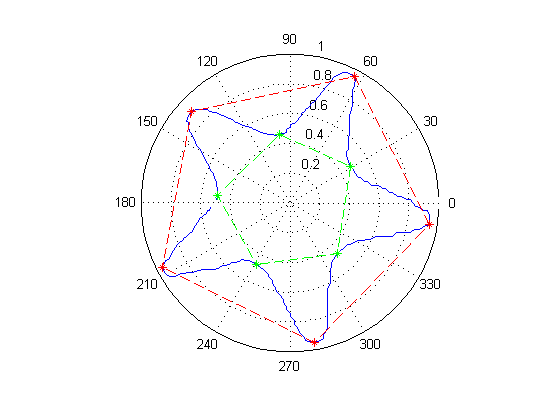
From this point on, the challenge it to determine what the signature corresponds to. For ease of viewing it is easiest to view the signal as plotted in polar coordinates. The image below shows the signal generated by the preceding script as a blue line.
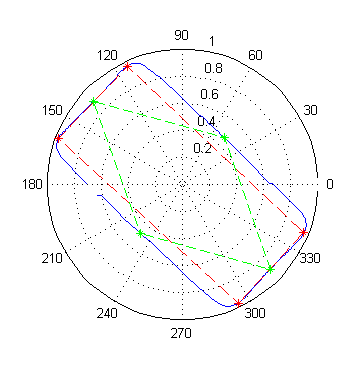
The method used to process theses images tries to find certain features in the signature; in particular, local maximums and minimums. Maximums indicate the location of an outside corner. Minimums indicate inside corners or the midpoints of lines that run past the centroid. A straight line will appear to get closer and closer to the centroid until it reaches a minimum and then begins to move away. In the case of the star all minimums are inside corners, but in the rectangle shown below, all minimums are the result of lines passing by the centroid.
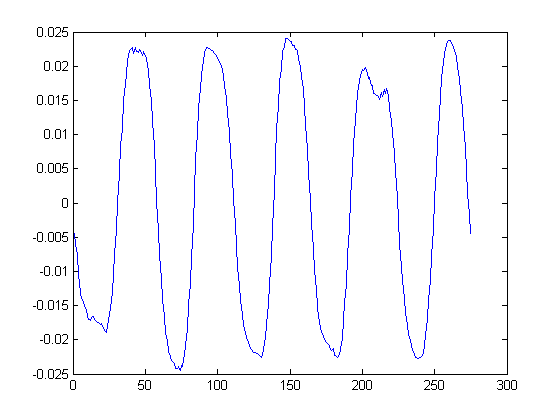
To find these points the instantaneous rate of change between each consecutive pair must first be calculated. This produces the below chart shown in Cartesian coordinates. Critical points are located at each point where the plot crosses the x axis. This point can be easily located by checking for a sign change.
Once the critical points have been located it is simply a matter of classifying the target. Circles are filtered out first by looking for cases where the max and min of the signature are very close together. Next, the classifier discriminates based on the number of critical points. This will be the final step for ovals and triangles. For the other shapes a comparison of the average maximum and minimum points values are compared. Star like shapes will have a much greater difference than regular shapes. Quadrilaterals undergo an additional check to compare the values of consecutive maximums. A large difference will indicate a diamond shape.
When run against a set of seven artificial targets, the method correctly identifies every shape. Running against the real image set sees excellent results as well. Moving forward it will be important to expand the data set to include more real images. There are some enhancements to the current algorithm that may make it more robust. It would also be interesting to explore the application of a neural net in solving the signature identification. One final advantage to this algorithm is speed. When just asked to determine the shape, the star image can be processed in less than half a second.
I’ve made the code available here as a download. It requires the use of the Mathworks Image Processing Toolbox to work, which I don’t have anymore, so the code is provided as is without testing.